基于 PCA 的人脸识别方法——特征脸法
1991 年的论文,提出了一种借助 PCA 方法进行有效人脸识别的方法——特征脸法。
思路:借助 PCA 分析主要成分,对人脸数据进行降维,再进行相关计算,以减少复杂度。
PCA 的几何解释
找到一组新的坐标轴,或者说是一组新的基(basis),用于表示原来的数据,使得在表示数据时不同轴是不相关的(即协方差为0)。
取出其中含有信息较多(即方差较大)的坐标轴(基),构成(span)一个新的空间,舍弃其他维度的信息。
由于新空间的维度小于原来的空间,所以把数据投影到新的空间后,可以大大降低数据的复杂度(虽然会损失少量信息)。
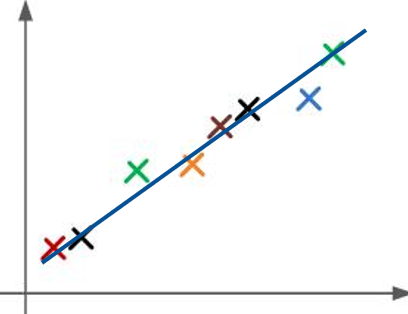
PCA 的大致思路
- 样本中心化:算出数据在每一个维度上的平均值,让该维数值减去这个平均值,中心化不会改变求得的新空间,但会减少计算量。
- 对中心化后的数据,算出这些数据的协方差矩阵。协方差矩阵的含义:第 i 行 k 列的值,表示 i k 对应的两个方向(坐标轴)的协方差。
对协方差矩阵进行对角化,即算出协方差矩阵的特征值与特征向量。
含义:对角化意味着非对角线元素为0,也就意味着不同坐标轴(不同方向)之间两两互不相关(协方差为0)。而协方差矩阵对角线上元素,就是数据在各个方向上的方差(也是特征值),方差越大意味着数据在这个方向上的散度越大,也就意味着这个方向包含的信息更多。
取特征值大的一些特征向量构成一个矩阵 P,这个矩阵是一个投影矩阵:能够把原始空间的数据投影到新的空间。
特征脸法的大致思路
数据预处理:将每一张人脸拉成一个列向量,所有人脸构成一个矩阵,每列是一张列。
求平均脸:对每一行都求平均值,得到一个列向量,我们称之为“平均脸”,是所有人脸的平均。下图是 YaleB 数据集求得的一张平均脸。

样本中心化:每一个脸都减去平均脸。下图是原始数据在减去平均脸后得到的中心化的数据。

对中心化后的样本,求协方差矩阵的特征向量。每一个特征向量都是一张脸,我们称之为“特征脸”(eigenface),原始的人脸可以表示为特征脸的线性组合。
比如,一张人脸图像可能是特征脸1的10%,加上特征脸2的55%,再减去特征脸3的3%。
下图把特征脸按照特征值大小排列,可以看到特征值大的脸,其包含的有效信息更多。
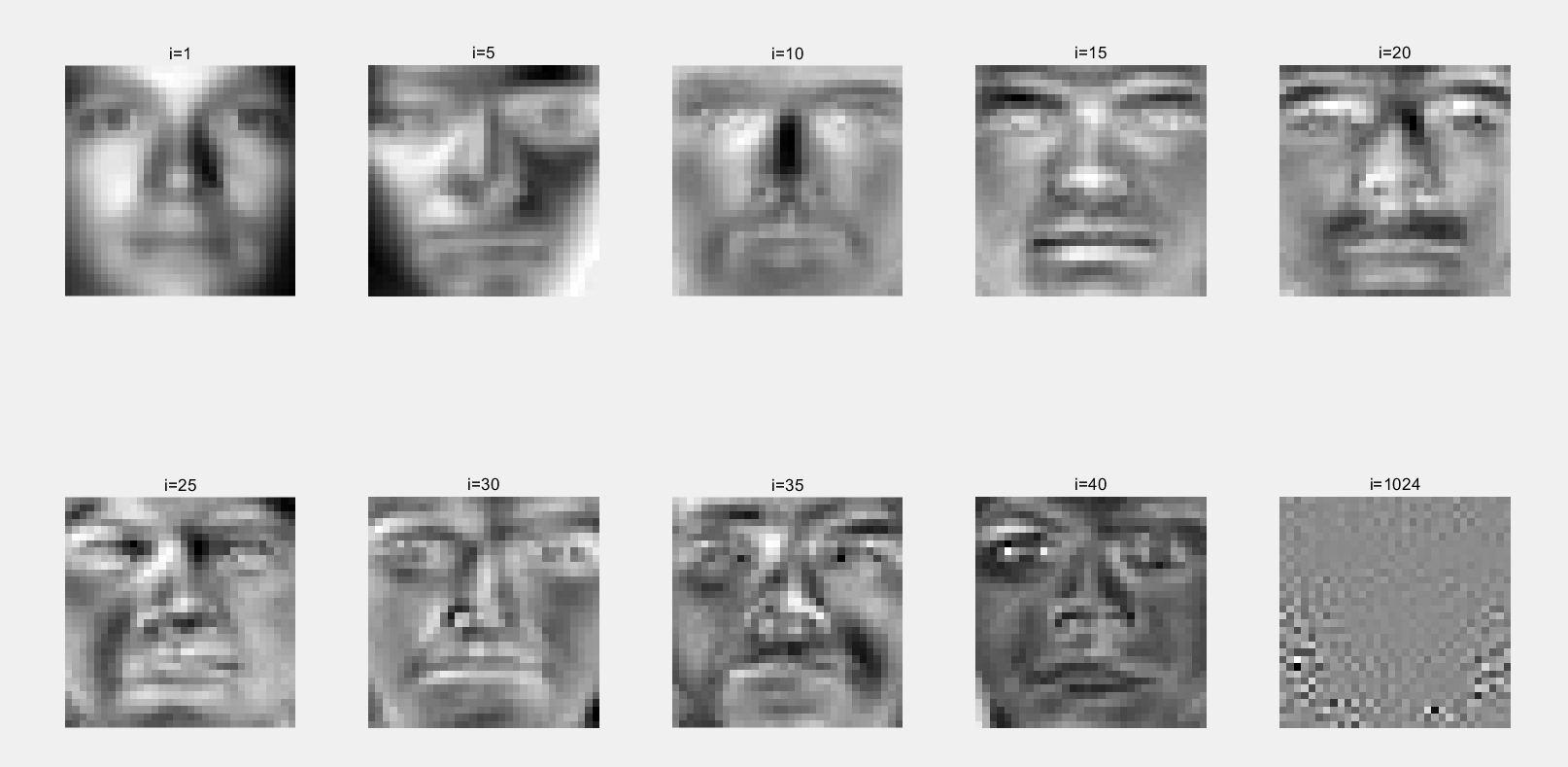
取出特征值较大的特征脸,构成投影矩阵。这个投影矩阵可以把人脸投影到一个子空间上,我们称之为脸空间(face space)。
把某个人的所有脸都投影到脸空间中,求均值,得到脸空间中的一个点,称之为这个人的“特征”(pattern vector)。以此类推,求出每一个人的“特征”,每一个特征代表一个人的脸。
现在有了一个待识别的人脸,只要把它也投影成子空间的一个点,看这个点和空间中哪个点(这个点代表某个人的脸)离得近,我们就认为这个脸是某个人的。
如果它和“最近的脸”离得太远,我们认为这张图象并不是一张脸。
特征脸法的具体计算细节
以 YaleB 数据集为例,进行分析。YaleB 数据集包含 2414 个人脸,每个人脸是 32x32=1024 大小。
数据预处理:读取数据集,“YaleB_32x32.mat”包含已经处理好的数据,含有一个 2414x1024 大小的矩阵,每行是一张人脸。
1
load('YaleB_32x32.mat');
计算平均脸:对每一列都求出一个平均值,最终得到一个 1024 维的行向量,即平均脸。
1
mean_face = mean(train_data, 1);
样本中心化:把原始数据每行是一个人脸,让每一行都减去平均脸,这里顺便做一次转置,与论文保持一致。转置后每一列是一张人脸。
1
centered_face = (train_data - mean_face)';
计算写协方差矩阵的特征值、特征向量
一般来说,计算协方差矩阵特征值和特征向量的方法是,先计算协方差矩阵,然后求其特征值和特征向量。但是这种方法的计算规模较大,所以论文提出了一种更加节省算力的方法——SVD,奇异值分解 - 维基百科,自由的百科全书 (wikipedia.org)。
论文给出了详细的推理过程,最终得出的结论是:计算 L = A’ * A ,而不是 Cov = A * A’ (Cov指的是协方差矩阵)。求出 L 的特征向量后,令其与前面求出的中心化数据 A 相乘后便可得到协方差矩阵的特征向量。
1 | % 这里L是协方差矩阵的替代 |
取出特征值较大的特征向量,作为特征脸。特征值的累加如下图所示,排位靠前的几个特征值占了总特征值的大部分:
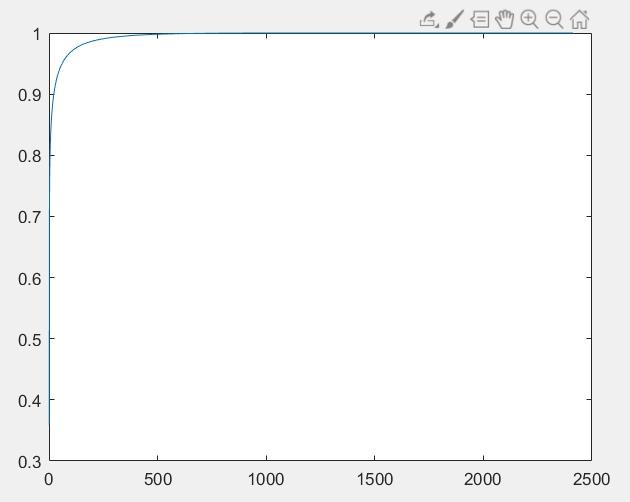
取出的特征向量构成投影矩阵,这个投影矩阵可以把人脸投影到一个子空间上,我们称之为脸空间(face space)。此后只要用投影矩阵去左乘数据,就能把数据投影到子空间中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24% 对特征值进行排序,获得排列后的特征值和索引
[sorted_eigen_values, index] = sort(eigen_values, 'descend');
% 获取排序后的征值对应的特征向量
sorted_eigen_vectors = eigen_vectors(:, index);
% 特征脸(所有)
eigen_faces = centered_face * sorted_eigen_vectors;
waitfor(show_faces(eigen_faces));
% 取出前90%的特征值对应的特征脸
order = 0;
sum_eigen_values = sum(sorted_eigen_values);
target_eigen_values = sum_eigen_values * 0.9;
for i=sorted_eigen_values'
count = count + i;
order = order + 1;
if (count < target_eigen_values)
break;
end
end
% 占90%特征值对应的约简后的特征脸
reduced_eigen_faces = eigen_faces(:,1:order);
把某个人的所有脸都投影到脸空间上,求平均后得到一个”pattern vector”。
1
2
3% 将已知人脸投影到脸空间中,即eigenface pattern vector
% 每列是一个人脸的特征向量
omega = reduced_eigen_faces' * centered_face;这里取出前五个人的人脸求平均值得到前五个人人的”pattern vector”,它代表了五个人的脸的特征:
1
2
3
4
5
6% 求5个人在脸空间中的pattern vector
omega_k_1 = mean(omega(:,1:63),2);
omega_k_2 = mean(omega(:,64:127),2);
omega_k_3 = mean(omega(:,128:191),2);
omega_k_4 = mean(omega(:,192:255),2);
omega_k_5 = mean(omega(:,256:319),2);假设现在有了一个新的人脸,想要知道它是谁的人脸。那么首先需要将其投影到脸空间中:
1
2% 新人脸投影到脸空间中
omega_new_face = reduced_eigen_faces' * (new_face - mean_face)';然后计算它和最近的点的距离,如果这个距离过大(阈值自主设定),那么我们可以认为它不是一张脸。
新的人脸投影到脸空间后,它实际上是脸空间中的一个点,其他已知人的“eigen pattern”也是一些脸空间的点。所以只要计算新的点与其他人的点的距离,如果这个点最接近 A 所属的点,那么我们就认为这个脸是属于 A 的。
1 | % 计算新的点与特征向量均值的距离(论文中称之为与脸空间的距离) |
计算距离的过程,求的是欧几里得距离,论文中表示为二范数(欧几里得范数),实际上就是初高中解析几何中常见的”求空间中两 点距离的方法”。1 | % 计算新的脸与五个人的脸的距离 |
参考资料
Eigenfaces for Recognition (mitpressjournals.org)
eigenfaces algorithm - File Exchange - MATLAB Central (mathworks.cn)
特征脸 - 维基百科,自由的百科全书 (wikipedia.org)
人脸识别之主成分分析(PCA) - 知乎 (zhihu.com)
本文地址: https://www.chimaoshu.top/基于PCA的人脸识别方法——特征脸法/
版权声明:本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议,转载请注明出处。