基于 PCA 的人脸识别方法——特征脸法[2]
前言
这次主要说说 Matlab 实现与可视化。上次用了 YaleB 数据集不够好用,每个人的人脸图片数量不同,导致训练数据和测试数据划分比较麻烦。这次换了ORL数据集,好了些。
PCA
- 数据读取与预处理,ORL数据集一共400张图,40人,一个人10张。每个人10张照片,取4张作为测试数据,6张作为训练数据。
1 | % 400张图,一共40人,一人10张 |
得到的训练数据和测试数据都是一个矩阵,每一列就是一张脸。通过提取训练数据中的部分列向量,重塑为方阵,并转化为灰度图像得到下图,代表了未经处理的原始数据,如图所示:

对训练数据的所有列向量求平均,得到平均列向量,将其重塑为图像即为”平均脸“,如图所示。由于该图像源于所有人脸的平均,所以直观上看可以看出人脸的轮廓,但五官细节较为模糊。
1
2% 求平均脸,即每一列分别求均值
mean_face = mean(train_data, 2);

将所有列向量减去平均列向量,得到中心化后的数据。将部分中心化后的列向量重塑后转化为灰度图像,即为中心化后的脸。由于减去了平均人脸,因此相比原始人脸,中心化后的人脸的灰度值更低,图像直观上显得更加暗淡。
1
centered_face = (train_data - mean_face);

求出协方差矩阵的特征值与特征向量,将特征向量按照特征值大小排序。下图是部分特征向量通过重塑后转化为灰度图像得到的特征脸。从直观上可以看出随着特征值的降低,对应的特征脸越来越模糊,这是因为特征值大的特征脸保留了更多的有效信息。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15% 协方差矩阵
cov_matrix = centered_face * centered_face';
[eigen_vectors, dianogol_matrix] = eig(cov_matrix);
% 从对角矩阵获取特征值
eigen_values = diag(dianogol_matrix);
% 对特征值进行排序,获得排列后的特征值和索引
[sorted_eigen_values, index] = sort(eigen_values, 'descend');
% 获取排序后的征值对应的特征向量
sorted_eigen_vectors = eigen_vectors(:, index);
% 特征脸(所有)
all_eigen_faces = sorted_eigen_vectors;

值得一提的是,这里也可以使用SVD的方式去求特征脸,详见上文。
- 取出第一张人脸,使用不同数量的特征向量进行重构。
1 | % 取出第一个人的人脸,用于重建 |
下图是分别在20,40,60,…,160数量的特征向量下重构的人脸。从直观上可以看出随着特征向量数量的增加,重构出的人脸越来越清晰。这是因为使用越多的特征向量进行人脸重构,丢失的信息越少,因此重构出的人脸更加清晰。

计算不同数量特征向量下,人脸的识别准确度,思路是:将人脸投影到低维空间中,计算未知人脸与所有已知人脸的距离(欧几里得距离),然后使用最近邻分类器KNN进行识别。最终的准确率在 93%-97% 之间。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80index = 1;
X = [];
Y = [];
for i=10:10:160
% 取出相应数量特征脸
eigen_faces = all_eigen_faces(:,1:i);
% 测试、训练数据降维
projected_train_data = eigen_faces' * (train_data - mean_face);
projected_test_data = eigen_faces' * (test_data - mean_face);
% 开始测试识别率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% KNN的k值
for k=1:6
% 用于保存最小的k个值的矩阵
% 用于保存最小k个值对应的人标签的矩阵
minimun_k_values = zeros(k,1);
label_of_minimun_k_values = zeros(k,1);
% 测试脸的数量
test_face_number = size(projected_test_data, 2);
% 识别正确数量
correct_predict_number = 0;
% 遍历每一个待测试人脸
for each_test_face_index = 1:test_face_number
each_test_face = projected_test_data(:,each_test_face_index);
% 先把k个值填满,避免在迭代中反复判断
for each_train_face_index = 1:k
minimun_k_values(each_train_face_index,1) = norm(each_test_face - projected_train_data(:,each_train_face_index));
label_of_minimun_k_values(each_train_face_index,1) = floor((train_data_index(1,each_train_face_index) - 1) / 10) + 1;
end
% 找出k个值中最大值及其下标
[max_value, index_of_max_value] = max(minimun_k_values);
% 计算与剩余每一个已知人脸的距离
for each_train_face_index = k+1:size(projected_train_data,2)
% 计算距离
distance = norm(each_test_face - projected_train_data(:,each_train_face_index));
% 遇到更小的距离就更新距离和标签
if (distance < max_value)
minimun_k_values(index_of_max_value,1) = distance;
label_of_minimun_k_values(index_of_max_value,1) = floor((train_data_index(1,each_train_face_index) - 1) / 10) + 1;
[max_value, index_of_max_value] = max(minimun_k_values);
end
end
% 最终得到距离最小的k个值以及对应的标签
% 取出出现次数最多的值,为预测的人脸标签
predict_label = mode(label_of_minimun_k_values);
real_label = floor((test_data_index(1,each_test_face_index) - 1) / 10)+1;
if (predict_label == real_label)
%fprintf("预测值:%d,实际值:%d,正确\n",predict_label,real_label);
correct_predict_number = correct_predict_number + 1;
else
%fprintf("预测值:%d,实际值:%d,错误\n",predict_label,real_label);
end
end
correct_rate = correct_predict_number/test_face_number;
X = [X k];
Y = [Y correct_rate];
fprintf("k=%d,i=%d,总测试样本:%d,正确数:%d,正确率:%1f\n", k, i,test_face_number,correct_predict_number,correct_rate);
end
end
waitfor(plot(X,Y));人脸投影到低维空间的可视化:分别将人脸投影到二维空间与三维空间,并画图。
1 | % 二三维可视化 |
效果:
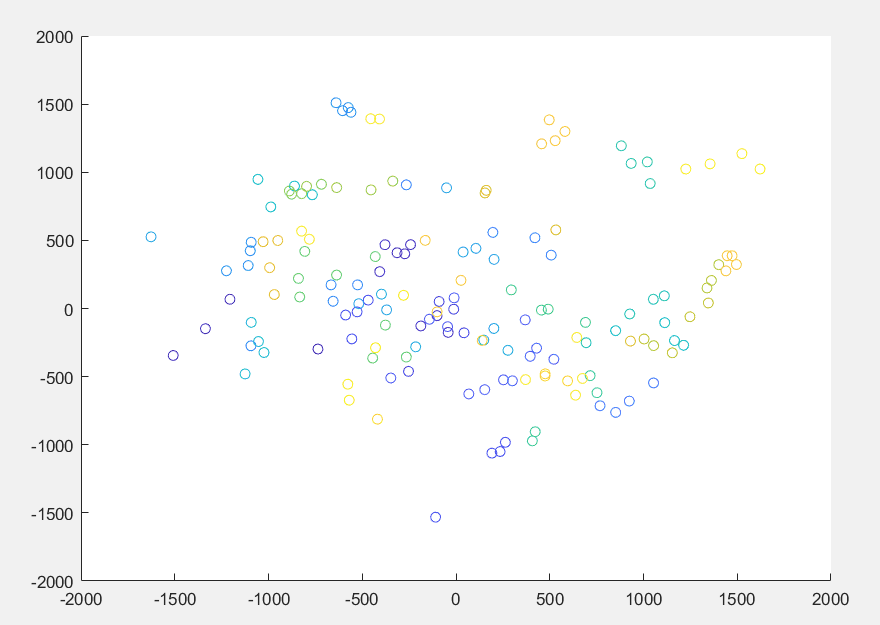
上图将人脸投影到二维空间下的可视化表示,每一个点代表一张人脸的图像,颜色相同的点代表同一个人的脸。
下面两图分别是在不同的两个角度下观察人脸数据在三维空间下的投影。其中每个点代表一张人脸图片,颜色相同的点代表同一人脸。由于同一人的人脸相近,因此颜色相同的点总是聚集地更加紧凑一些。
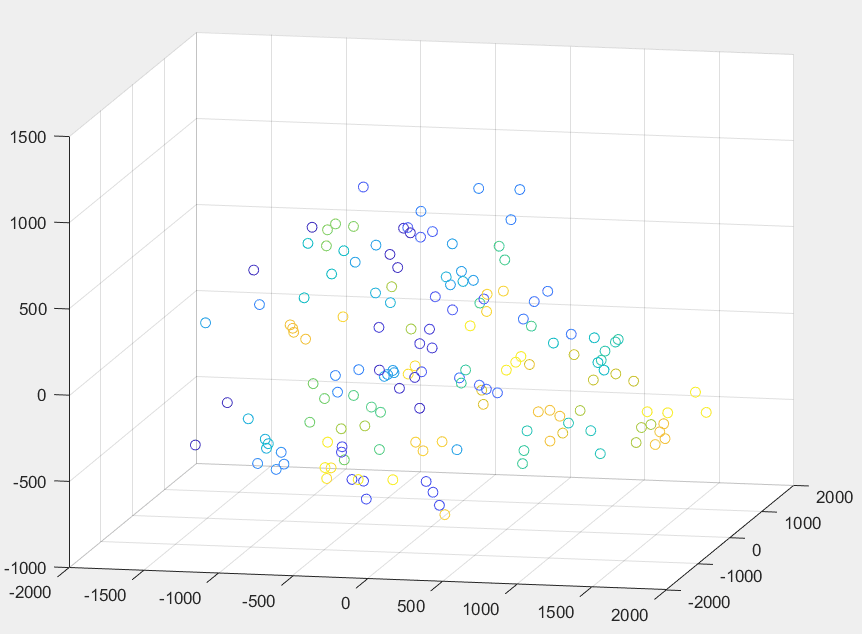
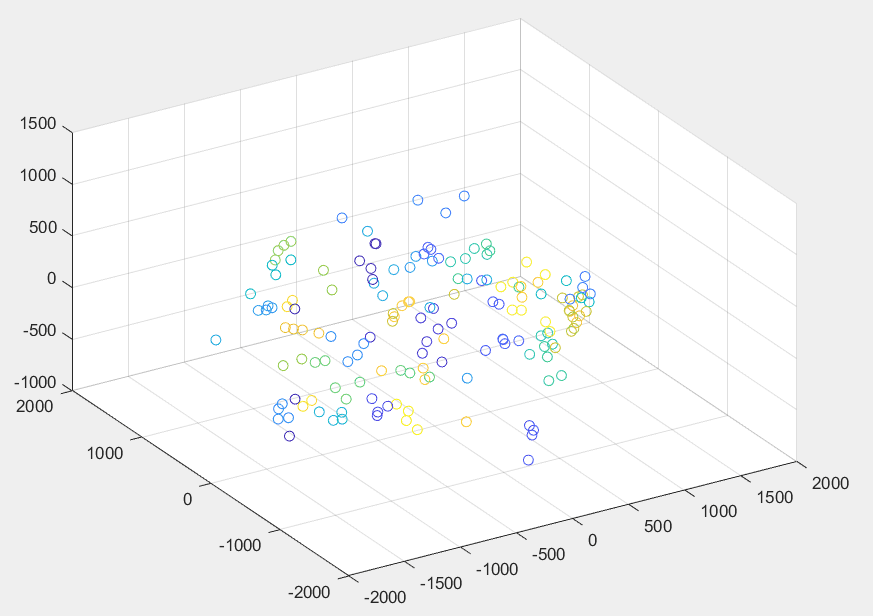
所有代码
1 | clear all; |
本文地址: https://www.chimaoshu.top/基于-PCA-的人脸识别方法-特征脸法-2/
版权声明:本博客所有文章除特别声明外,均采用 Apache License 2.0 许可协议,转载请注明出处。